When I first started selling options, the biggest question I had was “how do I decide if a trade is good or not?” The option sellers I was following at the time recommended a rule of thumb which balanced the MAX gain and MAX loss for a given trade, along with their associated probabilities.
This rule of thumb was the expected value. In statistics, expected value is used to compare all the possible outcomes of an event by their values and probabilities of occurrence in order to determine the long term outcome of experiencing that event many times.
For example, imagine a game involving coin flips. Each side of the coin has a 50% chance of occurrence. Let’s say you make $100 dollars every time the coin lands on heads and you lose $100 every time it lands on tails. Should you play this game?
Expected value can help you answer this question, but since this is a very simple case, let’s first think about it intuitively. If each outcome (win or loss) has the same probability of occurrence, and the amount of money you win or lose is the same in each case, then you would expect your net profit to be zero after many coin flips because presumably you would have experienced an equal number of heads and tails, and so you would have won $100 and lost $100 the same number of times.
Consider a less obvious scenario. Say the coin has a 70% chance of landing on heads, in which case you win $100, and it has a 30% chance of landing on tails, in which case you lose $150. Should you play this game? When the numbers are not as straightforward as the first example, or there are more than two possible outcomes, the expected value formula comes in handy.
Expected value is the sum of all possible outcomes, with each outcome being the product of its value and probability of occurrence.

In this formula, “x” is the value of a given outcome, and “p” is the probability of that outcome occurring. Note that all the probabilities have to add to 1 (100%), so you have to include every possible outcome in the calculation.
In the simple case of a coin flip, there are only two possible outcomes, so this formula can be reduced to two terms.
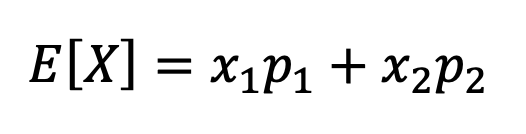
To solve the 70/30 coin flip scenario, we can plug in the values as follows:

This means that in the long term, if you keep playing this game over and over again, you can expect your average winnings to be $25 per coin flip. In reality, you will not win $25 on each coin flip, but after many flips, if you take your net earnings and divide them over the number of flips, it would be as if you won $25 on each flip.
Expected value can apply to selling options as well. Imagine selling a call credit spread on ticker XYZ currently trading at $100 per share, and your spread consists of a $110 short call and $120 long call. Let’s assume you collect $5.00 (per share) in premiums. In this scenario, assuming you hold the spread until expiration, you will win if XYZ closes below $110 at expiration. Your winnings will be the net premium you collected when you sold the spread, or $500.
On the other hand, if XYZ closes between $110 and $120, your net loss will be XYZ’s closing price minus $110 (times 100 shares), minus the net option premium, which you still get to keep. If XYZ closes at or above $120, you will lose exactly $1000 ($10 per share) minus the premium, which you still get to keep.
Although there are nearly an infinite number of possible closing prices, we can simplify this situation and use expected value to get an idea of whether or not it is a good trade. Let’s assume there are only two possible outcomes – a total win or a total loss, and let’s assume some probabilities for those outcomes.
| Outcome | XYZ Closing Price | Probability | Net Premium | Losses | Net Profit (*100 Shares) |
| Total Win | $110 | 70% | +$5 | $0 | +$500 |
| Total Loss | $120 | 30% | +$5 | -$10 | -$500 |
We can calculate the expected value for this trade as follows:
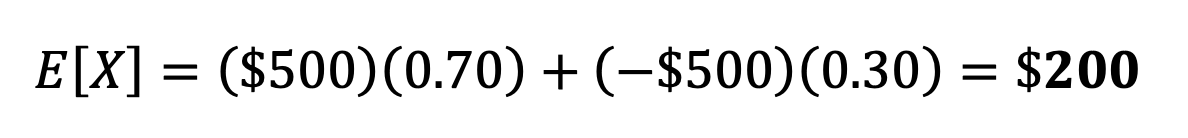
This means this trade is expected to profit $200 each time, on average, in the long term, if the same type of trade is executed many times over. The formula tells us that this is a winner. However, this is just an example. Good luck finding this spread selling for $5.
From the perspective of an option seller, it would be helpful to be able to quickly evaluate a trade to determine whether it is likely to profit on average in the long term. To do this, we can derive a formula to calculate the minimum premium you would need to collect for a given spread to break even on that type of trade in the long term.
Define variables:

Formula for expected value:

Re-arrange in terms of the credit (x1) so we can calculate the credit required to meet our criteria.
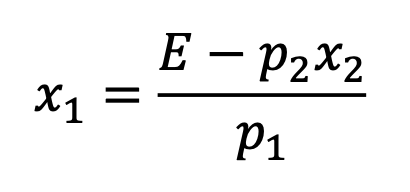
Since the MAX win is just the credit received…

Since you get to keep the credit no matter what, the MAX loss is actually…
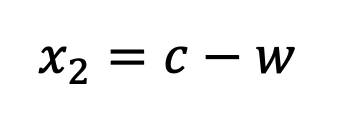
Substituting these expressions into the formula…
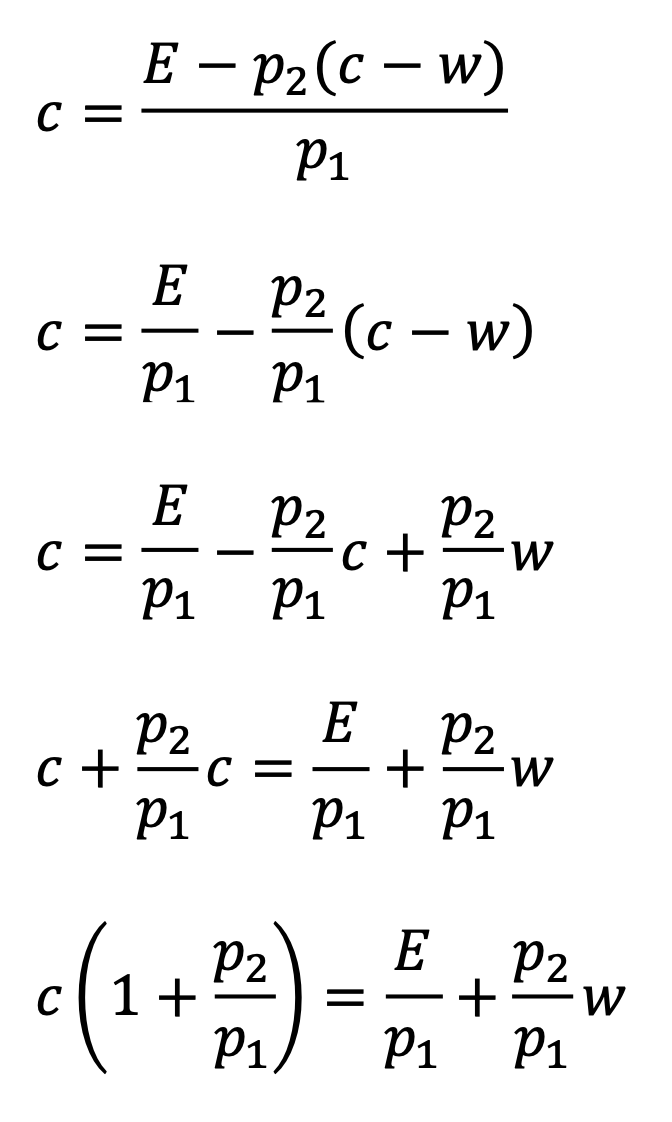
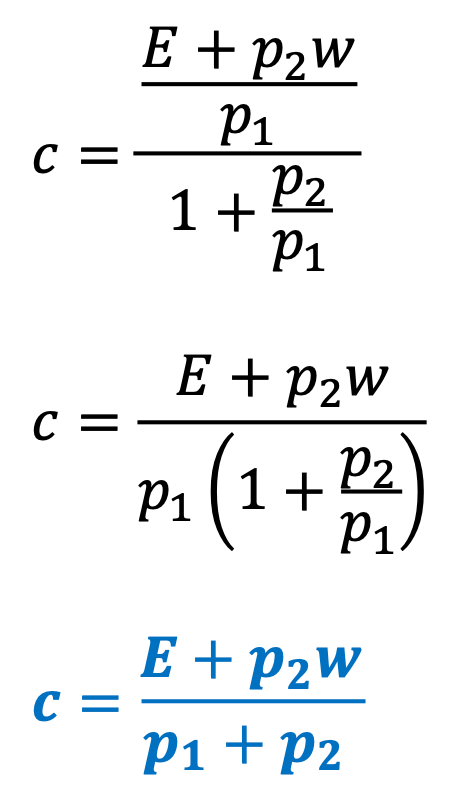
To calculate the minimum credit required to break even, simply set E=0. To use a stricter criteria, simply set E equal to whatever average profit per trade you are targeting. Unfortunately, you will be constrained by what the market offers you, so you have to be realistic.
Theoretically, if the trade pays a higher credit than the minimum “c” required, then it could be considered a good trade. Of course, there are several other factors to consider, such as upside potential vs. downside risk, sequencing risk (risk of getting a bunch of losers in a row and going bankrupt), and the fact that it is not advisable to not hold options until expiration, so modeling a trade assuming it will be held until expiration is not entirely accurate.
Furthermore, as previously mentioned, there are more than two possible outcomes to selling a credit spread because the stock could close at any price. I will explore a more realistic way of modeling this in a future post using a Monte Carlo simulation.
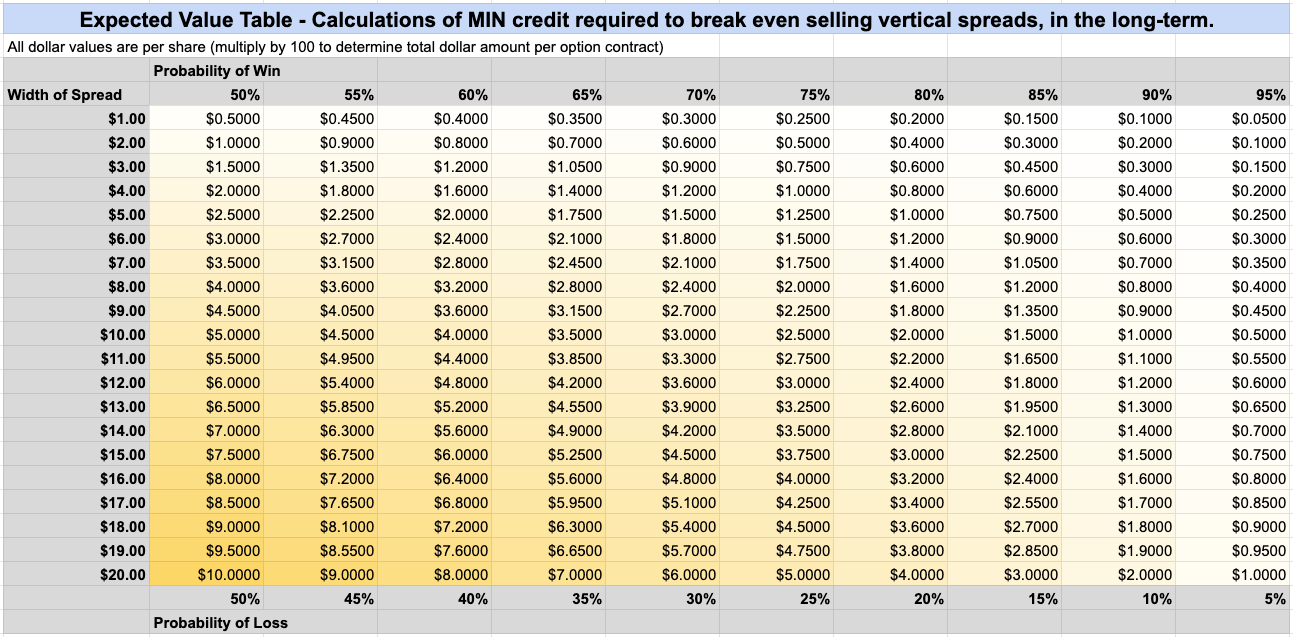
In any case, I used this “minimum credit” formula to create a reference table of common values for the types of trades that I often see when I’m browsing the option tables. This table can be used to quickly check what minimum premium would be required to break even on a spread with a given width, probability of total win, and probability of total loss.
Below is a screenshot, and the full spreadsheet can be downloaded here.
Thanks for reading! §