This is part 1 of the 3-part post on Monte Carlo simulations for option selling.
Jump to:
In my previous blog post on Expected Value, I showed how that simple formula could be used as a rule of thumb to estimate whether selling a given option spread is expected to be a “good trade.” However, one critical shortcoming of that formula was that only two discrete outcomes could be tested, a total win or a total loss. In this post, I will demonstrate a Monte Carlo simulation that I created to address this gap in the analysis.
A Monte Carlo Simulation is an iterative calculation that is used to model outcomes that can not be easily calculated analytically because their causes or probabilities are complex or interrelated. Let’s go back to the example from my Expected Value post to make this more clear:
Imagine selling a call credit spread on ticker XYZ currently trading at $100 per share, and your spread consists of a $110 short call and $120 long call. Let’s assume you collect $5.00 (per share) in premiums. In this scenario, assuming you hold the spread until expiration, you will win if XYZ closes below $110 at expiration. Your winnings will be the net premium you collected when you sold the spread, or $500.
On the other hand, if XYZ closes between $110 and $120, your net loss will be XYZ’s closing price minus $110 (times 100 shares), minus the net option premium, which you still get to keep. If XYZ closes at or above $120, you will lose exactly $1000 ($10 per share) minus the premium, which you still get to keep.
Because there are an infinite number of possible closing prices, each with its associated probability, it is not straightforward to analytically calculate the expected value for this situation. However, we can split the field of possible closing prices into a few hundred or a few thousand outcomes and then train a computer to calculate the profit or loss for each one.
We have two choices here. First, we could calculate the expected value using the entire array of outcomes. We could calculate the probability of every closing price between $110 and $120, multiply each one by its net profit/loss, and then add all those values up to see what the average profit/loss is expected to be on each trade in the long term.
The second option is, instead of going through each possible closing price sequentially, we could generate “simulated” closing prices according to the probability distribution that describes their individual likelihoods, and then just add up all the profits and losses to see if we come out ahead.
I built a tool to do this here.

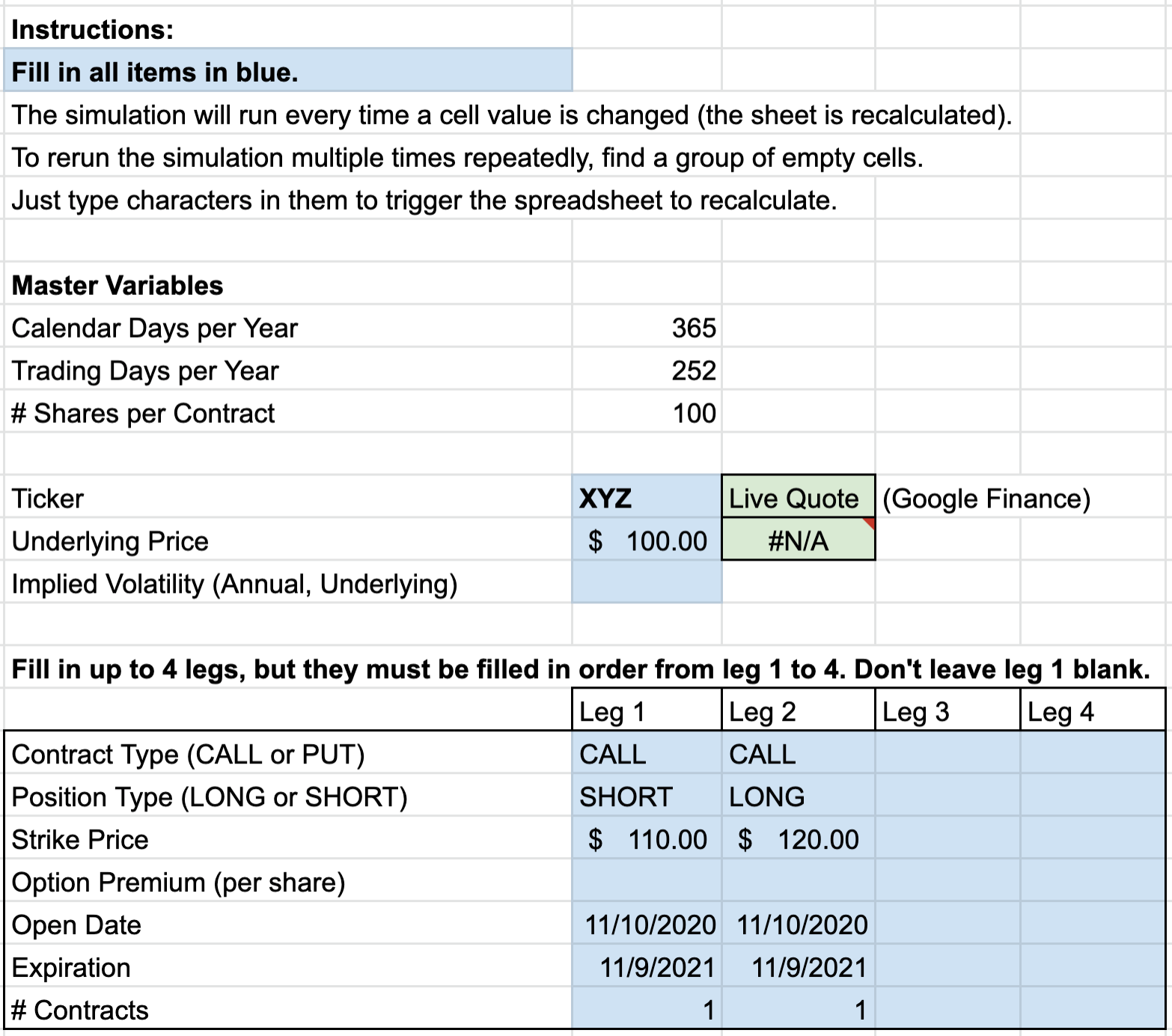
This spreadsheet will take option data for a spread with up to 4 legs and run a Monte Carlo simulation to see what the overall profit/loss would be in an account that starts with $10,000 and makes this same trade 1,000 times. Let’s walk through an example of how to use this tool for a call credit spread.
Let’s start by entering the data for the XYZ example above. We will assume a 1 year option term, starting on 11/10/2020 and ending on 11/9/2021. Note that if we were simulating a real stock, we could type the ticker symbol in the green box to pull a live quote from Google Finance.
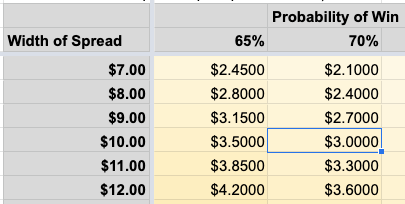
Since we don’t know what premium we would take in for this hypothetical trade, let’s use the expected value table to assign a premium that the expected value formula tells us should make a good trade. (See my other post “Expected Value for Option Sellers” to see how this table was created).
Let’s assume the long strike ($120) is at the 0.3 delta with a ~70% chance of being OTM at expiration. This means there is a 30% chance of a total loss. The expected value table tells us that with a spread width of $10, we would need to take in a net premium of at least $3.00 per share for this trade to break even in the long run.
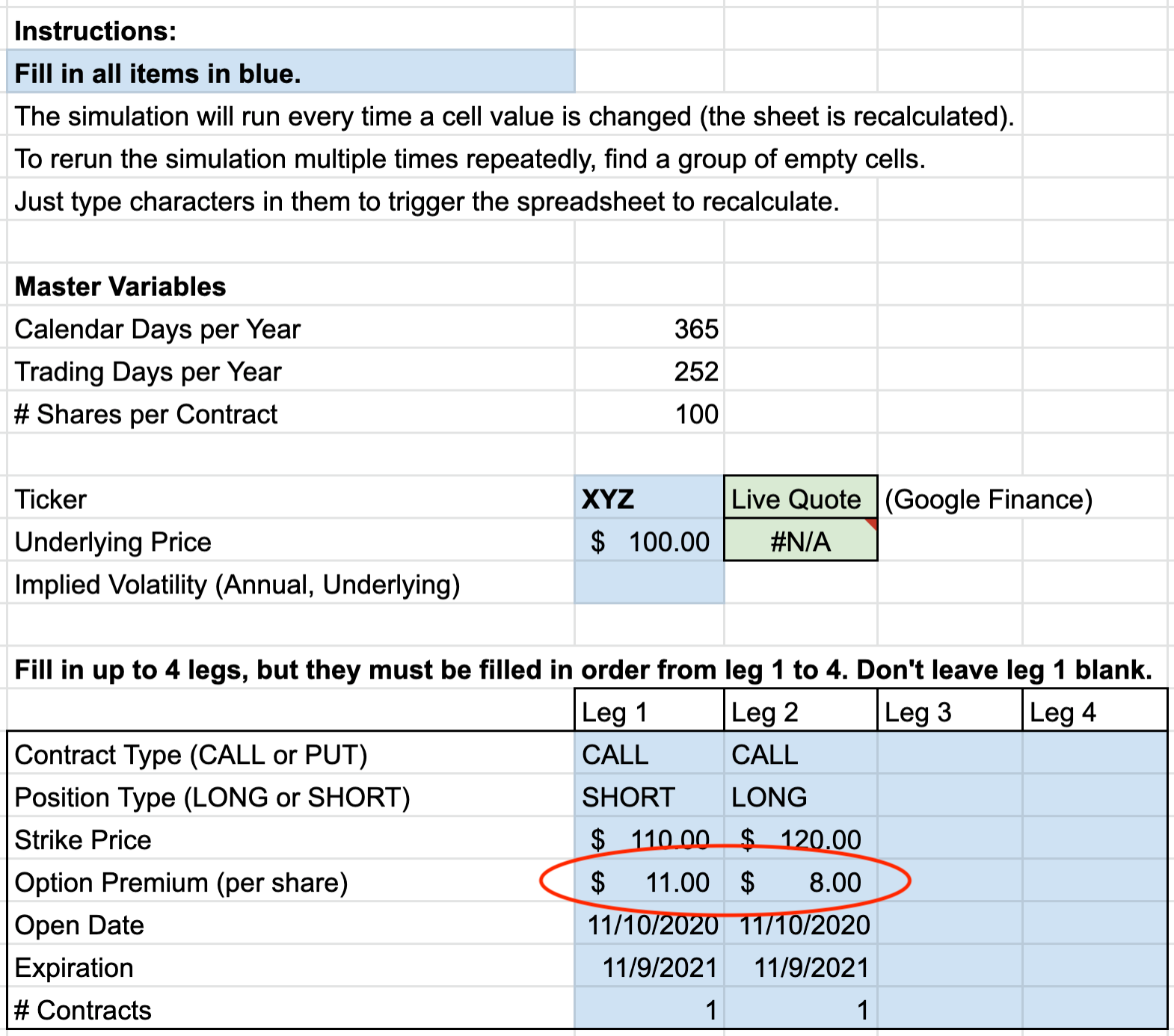
Let’s test this break-even premium in the simulation. If the expected value rule works properly, we should expect the net profit after many trades to be zero because we are just breaking even. We will choose arbitrary prices of $11.00 and $8.00 for the short and long strikes respectively, to achieve a $3.00 net credit for the spread.
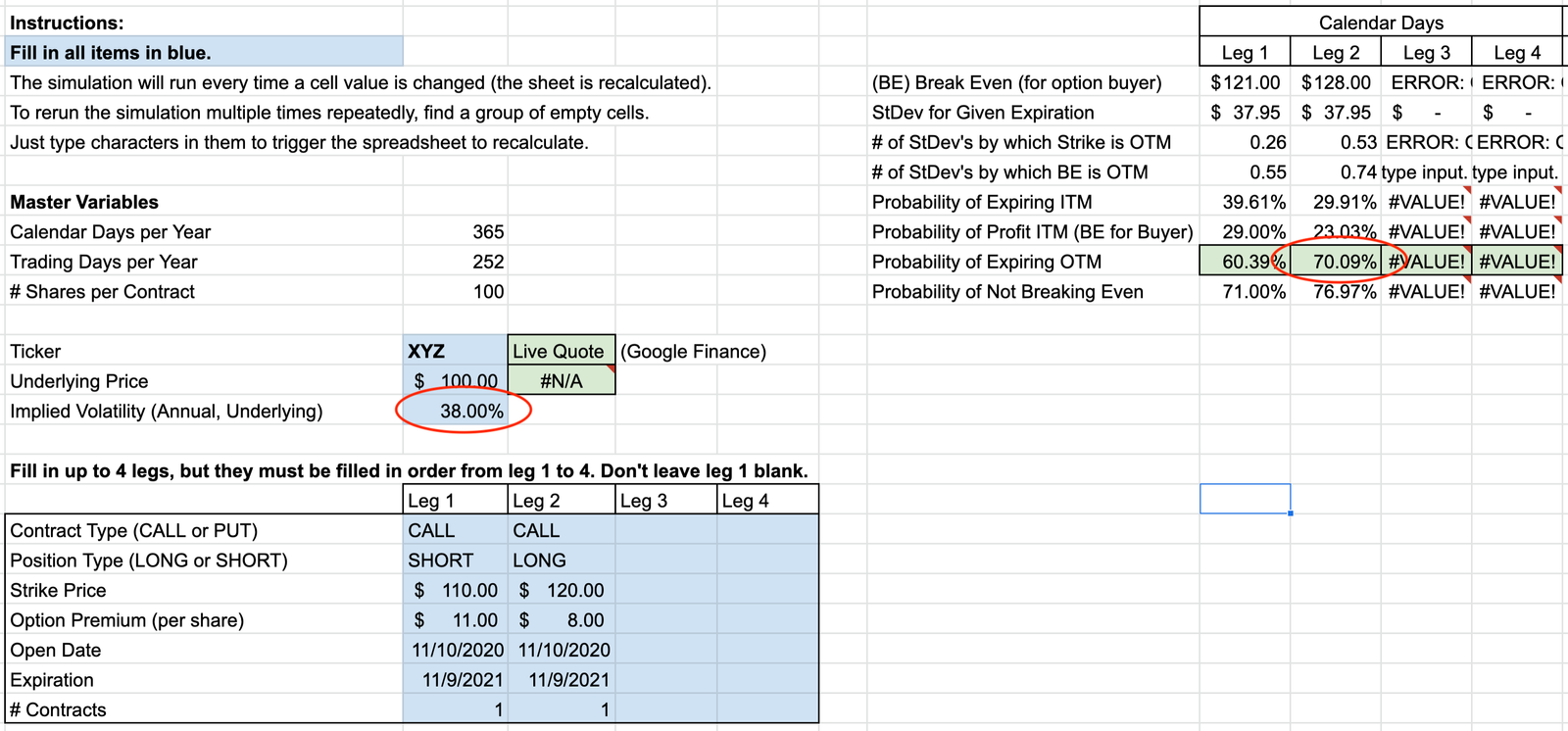
We will also need the implied volatility. Since there is no IV for this hypothetical stock XYZ, we will plug values into the calculator until we get ~70% probability of the long strike being OTM at expiration. The IV (annual) winds up being 38%.
(By the way, ignore the “ERROR” and “#VALUE” warnings in the unused cells – this just means we are not using legs 3 and 4 of the simulation, but the math will still work).
Now that we have all the inputs we need, our simulation is ready to run. In fact, it has already run and we just need to look at the results.
In part 2 of this study, I will show how the simulated trades were calculated, and in part 3, I will show the results.
Thanks for reading! §